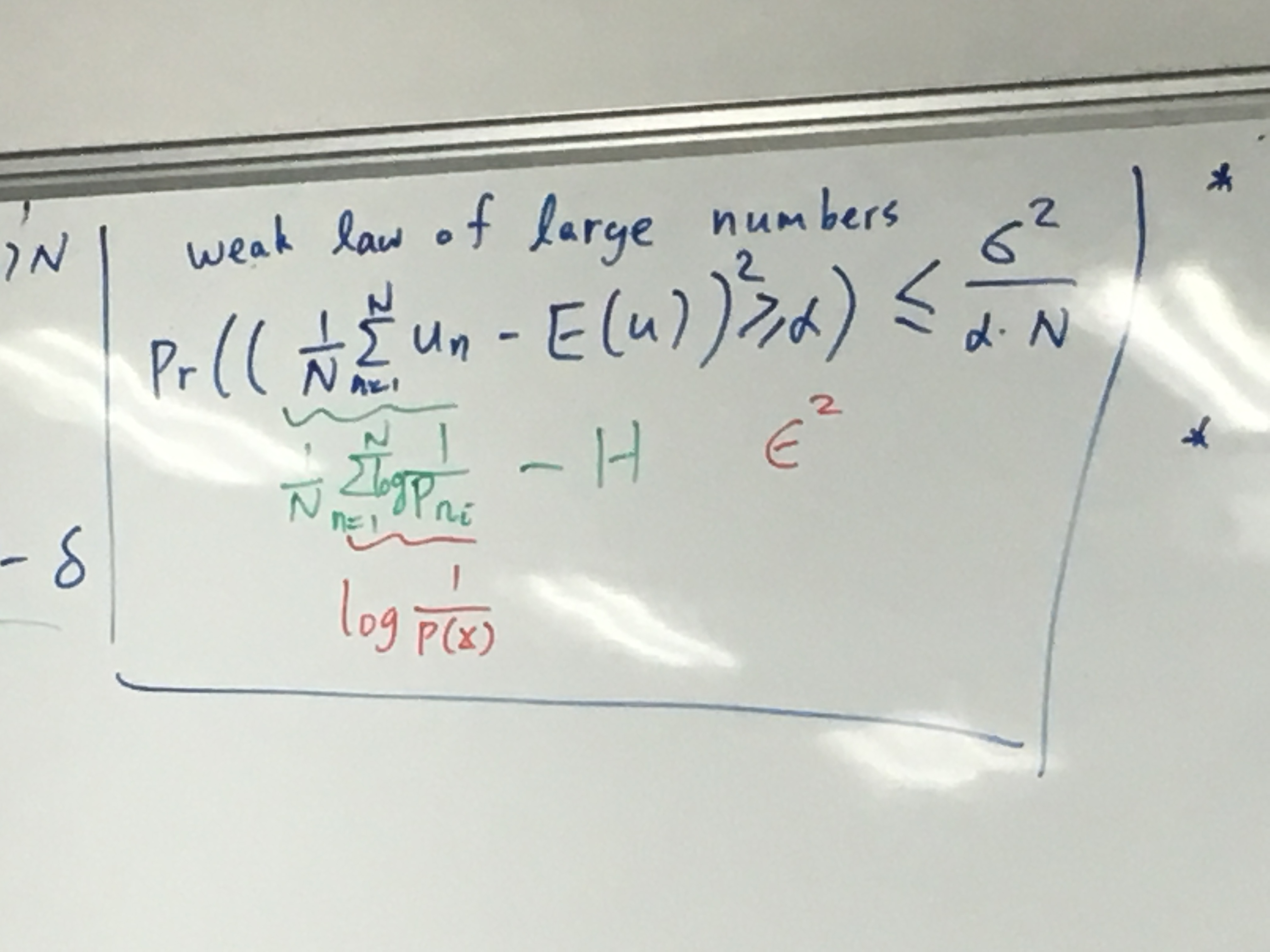[TOC]
Here is a table:
If there’s a unknown answer which might be 0,1, 2 or 3, by known which column contains it , we can get to know what it exactly is.
e.g. it in M : Answer is 1.
e.g. it in P and M : Answer is 3.
Now we can call the bold Alternatives as “Information”, for it lead us from uncertainty to certainty Outcome
There’s a finite set of such alternatives :
Z = { a 1 , a 2 , ⋯ , a n } \mathbb{Z}={\{a_1,a_2,\cdots,a_n\}} Z = { a 1 , a 2 , ⋯ , a n } each alternatives has these attribution:
Alternative: Uncertain possibilities Abstract: Not physical but universal Bidirectional: Currently the info. do not change from sender to receiver ( Dr. Lin also do not know why this attribution is necessary here, it has connection with further course. There still some argument why the Answer is 1 then we can know the pre-info. is M ) Additive: Given info. A, and info. B equals given info.(A+B) Now, define K:
H 0 ( { a 1 , a 2 , ⋯ } ) = l o g 2 K = l o g ( Z ) H_0({\{a_1,a_2,\cdots\}})=log_2K=log(\mathbb{Z}) H 0 ( { a 1 , a 2 , ⋯ } ) = l o g 2 K = l o g ( Z ) H 0 H_0 H 0 Z \mathbb{Z} Z
if X 鴿子 \mathbb{X}鴿子 X 鴿子 Y 籠子 \mathbb{Y}籠子 Y 籠子 X \mathbb{X} X Y \mathbb{Y} Y
X: Alternatives
Y: Names
One-to-one: e n c o d e r : v ( x ) → ∀ a 1 ! = a 2 , v ( a 1 ) ! = v ( a 2 ) encoder: v(x)→\forall a_1 != a_2 , v(a_1)!=v(a_2) e n co d er : v ( x ) → ∀ a 1 ! = a 2 , v ( a 1 )! = v ( a 2 ) ∃ d e c o d e r : μ ( x ) → μ ( v ( a ) ) = a \exists decoder:\mu(x) → \mu(v(a))=a ∃ d eco d er : μ ( x ) → μ ( v ( a )) = a
證明題:
由於鴿籠理論 Hdelta(X) > H0(Y)
那麽沒有 v 和 u(deterministic) 使得:
在H δ H_\delta H δ δ \delta δ
證明 :
如果存在 v 和 u 使得等式成立
所有正確的符合等式的 x 是 Hdelta 裏面的大集合 X ,X 的剩下部分在 decode 和 encode 后會壞掉,小於等於 delta 的部分
由於鴿籠 pri,鴿子一定要比籠子少 → 因爲正確集合的性質是在 enc 和 dec 全對,那由於鴿籠,它的量(x 的正確集合,也就是下圖的綠框)肯定比 Y 籠子的量小。
。則 H0(Y)>=log(x 的正確集合的數量)>=Hdelta(X),就可以證明 H0(Y)>=Hdelta(X),則原條件有問題,反證法得證。
log(x 的正確集合的數量)=H0(x 的正確集合的數量)
//// 因爲正確集合的性質是在 enc 和 dec 全對,那由於鴿籠,它的量肯定比 Y 籠子的量小。
n! Alternatives needs T(log(n!)) to create each Names .
H 0 H_0 H 0 NO. one-to-one can not be built, we can’t hold 0-error.(Pigeon hole principle)
YES, if some error?
e.g. Here are 10 balls , 1 of them is heavier. If we use a balance to measure , can we measure 2 times to get 0-error outcome? No
However, if we just throw the first ball, we can archive that. and we have 1/10 possibility to fail.
Now clear P :
U ⊆ X , P r ( U ) = ∑ a k ∈ U P ( a k ) U\subseteq \mathbb{X},P_r(U)=\sum_{a_k\in U}P(a_k) U ⊆ X , P r ( U ) = a k ∈ U ∑ P ( a k ) U: event
as for H σ ( X = l o g ∣ U ∣ : U ⊆ X , P r ( U ) > = 1 − σ H_\sigma(\mathbb{X}=log|U|: U\subseteq\mathbb{X},P_r(U)>=1-\sigma H σ ( X = l o g ∣ U ∣ : U ⊆ X , P r ( U ) >= 1 − σ
so:
H δ ( X ) = l o g ( m i n ( ∣ U ∣ : U ⊆ X , P r ( U ) > = 1 − δ ) ) H_\delta(\mathbb{X})=log(min(|U|:U\subseteq\mathbb{X},P_r(U)>=1-\delta)) H δ ( X ) = l o g ( min ( ∣ U ∣ : U ⊆ X , P r ( U ) >= 1 − δ )) We call it as Probabilistic info.
back to e.g. : H 1 / 10 < = l o g 9 H_{1/10}<=log9 H 1/10 <= l o g 9
X \mathbb{X} X P ( a k ) > 0 P(a_k)>0 P ( a k ) > 0 a k a_k a k
*When we throw everything , we get H 1 H_1 H 1
Thus , define δ < 1 \delta<1 δ < 1 0 < = H δ < = H 0 , ∣ U ∣ > = 1 0<=H_\delta<=H_0, |U|>=1 0 <= H δ <= H 0 , ∣ U ∣ >= 1
從上面的我們知道 Hdelta 是一個函數,Shannon Entropy 就是 Hdelta 的 summa number,它來總結整個函數的情況。
Hdelta 函數 在 delta=0 的時候等於 H0,在 delta 無限大的時候 Hdelta=0。 定義域 0,無限大。 對應域(0,H0),而且一定單調
entropy 評價對某個 Hdelta,代表的 case 下信息分散的程度。
假設現在大 X 集合是 a1,a2,a3。設它們對應的概率是 p1,p2,p3..(比方説你在 case:a1,的單選題中有 p1 的概率答對,也就是説你有 1/p1 個選擇。),a1,a2,a3..是你選對的那道題。要做對 a1,需要 log(1/p1)個 bit。
對於這個大 X 集合的 summary number,每個需要的 bit 量的加權平均值就是 Entropy。
Entropy 可以表現你這整套試卷(X \mathbb{X} X
S h a n n o n E n t r o p y : H ( X ) = ∑ P i ∗ l o g 2 ( 1 / p i ) Shannon Entropy:H(\mathbb{X})=\sum P_i *log_2{(1/p_i)} S hann o n E n t ro p y : H ( X ) = ∑ P i ∗ l o g 2 ( 1/ p i ) H 函數輸入集合大 X,返回它的 entropy。
注意:lim(x→)log(1/x)→0
對於絕對,p=1,H0=0(要知道一定發生的事情需要的信息量是 0bit)
證明 H < = H 0 H<=H0 H <= H 0
→
∑ P i L o g ( 1 / p i ) − ∑ P i l o g K < = 0 \sum P_i Log(1/p_i) -\sum P_ilogK<=0 ∑ P i L o g ( 1/ p i ) − ∑ P i l o g K <= 0 →
∑ P i ( l n ( 1 / p i ∗ K ) / l n 2 ) \sum P_i (ln(1/p_i*K)/ln2) ∑ P i ( l n ( 1/ p i ∗ K ) / l n 2 ) for l n θ < = θ − 1 ln\theta <= \theta -1 l n θ <= θ − 1
∑ P i ( l n ( 1 / p i ∗ K ) / l n 2 ) < = ( 1 / l n 2 ) ∑ P i ( ( 1 / P i ∗ K ) − 1 ) = 0 \sum P_i (ln(1/p_i*K)/ln2) <= (1/ln2)\sum P_i((1/P_i*K)-1)=0 ∑ P i ( l n ( 1/ p i ∗ K ) / l n 2 ) <= ( 1/ l n 2 ) ∑ P i (( 1/ P i ∗ K ) − 1 ) = 0 當 Pi=1/k 的時候等式成立(全部 ai 的幾率相等)
如果一個系列的 ai,它的 p 是兩個步驟來決定的,有 p 的概率做第一步的選擇,q 概率做第二個。我們把上面的 pi 換成p i ∗ q i j p_i*q_{ij} p i ∗ q ij
→
H ( X ) = ∑ 合法 i j ( p i q i j l o g ( 1 / p i q i j ) H(\mathbb{X})=\sum_{合法ij}(p_iq_{ij}log(1/p_iq_{ij}) H ( X ) = 合法 ij ∑ ( p i q ij l o g ( 1/ p i q ij ) →
= ∑ i p i ∑ q i j l o g ( 1 / q i j ) + ∑ ( p i q i j ) l o g ( 1 / p i ) ( 最後的 q i j 是 1 ,去掉后就只有 p i ) =\sum_ip_i\sum q_{ij}log(1/q_{ij})+\sum(p_iq_{ij})log(1/p_i) (最後的q_{ij}是1,去掉后就只有p_i) = i ∑ p i ∑ q ij l o g ( 1/ q ij ) + ∑ ( p i q ij ) l o g ( 1/ p i ) ( 最後的 q ij 是 1 ,去掉后就只有 p i ) 上式説明了 entropy 的可加性。
= ∑ i P i ∗ H ( X i ) + H ( X t o p ) =\sum_i P_i* H(\mathbb{X}_i)+H(\mathbb{X}_{top}) = i ∑ P i ∗ H ( X i ) + H ( X t o p ) 推廣:
H(X*X)=2H(X)
H σ ≈ H H_\sigma \approx H H σ ≈ H Imagine H σ ( X n ) H_\sigma(\mathbb{X}^n) H σ ( X n ) H ( X n ) H(\mathbb{X}^n) H ( X n ) H σ ≈ H H_\sigma \approx H H σ ≈ H
→ ( 1 / N ) H σ ( X n ) ≈ H ( X ) (1/N) H_\sigma(\mathbb{X}^n) \approx H(\mathbb{X}) ( 1/ N ) H σ ( X n ) ≈ H ( X )
s.t : TO PROVE : 1 / N ∗ ∑ i = 1 N l o g ( 1 / P k i ) ≈ H ( X ) 1/N*\sum_{i=1}^Nlog(1/P_{ki})\approx H(X) 1/ N ∗ ∑ i = 1 N l o g ( 1/ P ki ) ≈ H ( X ) l o g ( 1 / p k ) log(1/p_k) l o g ( 1/ p k )
左側相當於是一套選擇題有 N 道題,做出其中一套答案的幾率為 P,左側相當於 1/N* log(1/P).
For example: 每道題有三個選項,A,B,C。隨機猜 A 的概率 30%,B 是 30%,C 是 40%。
根據統計學知識,答案中 A 的個數會收束在 0.3N 上,B,C 同理。假設約等成立,則產生其中一個答案的概率 P 約等於2 − N H 2^{-NH} 2 − N H
這裏大 P,記作P = P ( Q 1 Q 2 Q 3 . . . Q n ) P=P(Q_1Q_2Q_3...Q_n) P = P ( Q 1 Q 2 Q 3 ... Q n )
( m a n y ) P ≈ 2 − N H ( 該式簡潔地揭露了 P 和 H 的聯係 , N 是測試的次數(也就是選擇題的個數) ) (many)P\approx2^{-NH} (該式簡潔地揭露了P和H的聯係,N是測試的次數(也就是選擇題的個數)) ( man y ) P ≈ 2 − N H ( 該式簡潔地揭露了 P 和 H 的聯係 , N 是測試的次數(也就是選擇題的個數) ) →
{ 2 N H P } ≈ 1 ( H 是 H ( X ) ) \{2^{NH}P\}\approx1 (H是H(\mathbb{X})) { 2 N H P } ≈ 1 ( H 是 H ( X )) →
N H ≈ H δ NH\approx H_\delta N H ≈ H δ **證明:**要證明約等,則要知道:
P r ( ( 1 / N ∑ n = 1 N u n − E ( u ) 2 ) > = α ) < = σ u 2 / α N Pr((1/N\sum^N_{n=1}u_n-E(u)^2)>=\alpha)<=\sigma_u^2/\alpha N P r (( 1/ N n = 1 ∑ N u n − E ( u ) 2 ) >= α ) <= σ u 2 / α N 也就是説左邊的平均概率和我們的 Expectation:E 的差大於 alpha 的概率(不等於),是小於平均方差
對於 random variable:r 和它的 expectation:E(r)
P r ( ( r − E ( r ) ) 2 > = α ) < = σ r 2 / α Pr((r-E(r))^2>=\alpha)<=\sigma_r^2/\alpha P r (( r − E ( r ) ) 2 >= α ) <= σ r 2 / α 相當於在求對一個 random variable: t :(t>=0)
P r ( t > = α ) < = E ( t ) / α Pr(t>=\alpha)<=E(t)/\alpha P r ( t >= α ) <= E ( t ) / α E(t)就相當於 r 的標準差σ \sigma σ
而標準差σ = ∑ P ( t ) / α \sigma=\sum P(t)/\alpha σ = ∑ P ( t ) / α
左邊則等於∑ P ( t ) [ t > = α ] \sum P(t)[t>=\alpha] ∑ P ( t ) [ t >= α ]
→
∑ P ( t ) [ t > = α ] < = ∑ P ( t ) t / α ( c h e b y s h e v ′ s I n e q u a l i t y ) \sum P(t)[t>=\alpha] <= \sum P(t)t/\alpha (chebyshev's Inequality) ∑ P ( t ) [ t >= α ] <= ∑ P ( t ) t / α ( c h e b ys h e v ′ s I n e q u a l i t y ) 現在討論約等號:
考慮實驗次數。
Given E>0 .
there exits N0 s.t.
N>=N0 → ∣ 1 / N H δ ( X n ) − H ( X ) ∣ < E |1/N H_\delta(\mathbb{X}^n)-H(\mathbb{X})|<E ∣1/ N H δ ( X n ) − H ( X ) ∣ < E
→
( 1 / N ) H δ ( X n ) < H ( X ) − E (1/N)H_\delta(X^n)<H(X)-E ( 1/ N ) H δ ( X n ) < H ( X ) − E 我們現在記 U 是 X 的一個子集,U 是一個大概率集
有
( 1 / N ) H σ ( X n ) < = ( 1 / N ) l o g ∣ U ∣ < H ( X ) + E (1/N)H_\sigma(X^n)<=(1/N)log|U|<H(X)+E ( 1/ N ) H σ ( X n ) <= ( 1/ N ) l o g ∣ U ∣ < H ( X ) + E U : Z : p ( z ) > 2 − ( H + E ) N U:{Z: p(z)>2^{-(H+E)N}} U : Z : p ( z ) > 2 − ( H + E ) N l o g ∣ U ∣ < ( H + E ) N log|U|<(H+E)N l o g ∣ U ∣ < ( H + E ) N 在 U 中,typically 一般出現的情況是 T,
以上的推論是想找出,通過覆蓋最常出現的選擇題回答的序列,來找到最少的 bit 讓我們可以得出 OUTCOME
*Shannon’s first theorem: 揭露了概率和熵的關係:
given 0 < e , o < δ 0<e , o<\delta 0 < e , o < δ
there exists no such that :
N > = N 0 − > H − e < ( 1 / N ) H δ ( X N ) < H + e ( 1 式 ) N>=N_0 -> H-e<(1/N)H_\delta(\mathbb{X}^N)<H+e (1式) N >= N 0 − > H − e < ( 1/ N ) H δ ( X N ) < H + e ( 1 式 ) 做了 N 次實驗的典型結果 T:
其 P(T)>1-σ 2 / e 2 N < δ \sigma^2/e^2N<\delta σ 2 / e 2 N < δ
(證明最上面的不等式,右半邊是用一個 T,T 的大小是在典型情況浮動, T 既然是 U 的子集合自然要小於 U。T 是典型集
左邊是假設有個 V,V 很小。V 有何 T 重合的部分,也有不屬於 T 的部分,那他們小於 T 對 X 的補集再加上 V 定義的數量(2 ( H − e ) N 2^{(H-e)N} 2 ( H − e ) N
整個不等式(1 式) 描述了 N 次實驗下H δ H_\delta H δ
現在我們知道
N > = N 0 − > H − e < ( 1 / N ) H δ ( X N ) < H + e N>=N_0 -> H-e<(1/N)H_\delta(\mathbb{X}^N)<H+e N >= N 0 − > H − e < ( 1/ N ) H δ ( X N ) < H + e 那對於典型集:
l o g ∣ 2 H δ + 1 ∣ ≈ H δ ≈ N H log|2^{H_\delta}+1|\approx H_\delta\approx NH l o g ∣ 2 H δ + 1∣ ≈ H δ ≈ N H 説明 N 次實驗需要 NH 來存,則每一次的典型情況都需要 H 個 bits 來記錄。我們就可以知道 Bit rate 差不多是 H。這叫 block coding:一次 decode N 次實驗的情況。Block 的長度就是 H。也就是H δ / N H_\delta/N H δ / N
Block coding 核心:(化成等长的块)
H δ ( X n ) ≈ b l o c k N H ( X ) H_\delta(X^n)\approx_{block} NH(X) H δ ( X n ) ≈ b l oc k N H ( X ) Symbol Coding 核心: 按照概率化成不等长的块(比如 haffman)
*realistic coding to archive H
symbol coding : x→v(x)
對於一系列 a1...ak 編碼成 v(a1)...v(ak),出現概率是 p1..pk,編碼長度是 n1...nk。
編碼后平均長度是
n a v e r a g e = ∑ p k n k n_{average}=\sum p_kn_k n a v er a g e = ∑ p k n k 現在證明某些情況下它約等於 block code length ≈ \approx ≈
-X
要做到 errorfree 編碼:UD (可解码编码)
就是要做到有
U D : ∑ k = 1 k 2 − n k < = 1 ( K r a f f ′ s ) UD: \sum_{k=1}^{k}2^{-n_k}<=1 (Kraff's) U D : k = 1 ∑ k 2 − n k <= 1 ( Kr a f f ′ s ) ↑ 也就是從 a1 到 ak,每個的長度要滿足上式。
→
U D f o r N = 1 : ∑ i = 1 上 ∣ { k : n k = i } ∣ ∗ 2 − i < = 上 UD for N=1 : \sum_{i=1}^上|\{k:n_k=i\}|*2^{-i}<=上 U D f or N = 1 : i = 1 ∑ 上 ∣ { k : n k = i } ∣ ∗ 2 − i <= 上 U D f o r N = 2 : ∑ i = 1 2 上 ∣ { k : n k + n e = i } ∣ ∗ 2 − i < = 2 上 UD for N=2 : \sum_{i=1}^{2上}|\{k:n_k+n_e=i\}|*2^{-i}<=2上 U D f or N = 2 : i = 1 ∑ 2 上 ∣ { k : n k + n e = i } ∣ ∗ 2 − i <= 2 上 上面證明了平均最短碼率是 Entropy.
現在考慮
H ( X ) − n a v e = ∑ p k l o g ( 1 / p k ) − ∑ p k n k H(\mathbb{X})-n_{ave}=\sum p_k log(1/p_k)-\sum p_k n_k H ( X ) − n a v e = ∑ p k l o g ( 1/ p k ) − ∑ p k n k →(因爲n k 是 l o g 2 n k n_k是log2^{n_k} n k 是 l o g 2 n k
= ∑ p k ( l n / l n 2 ) ( 2 − n k / p k ) < = ∑ p k ( 2 − n k / p k − 1 ) ( 因爲 x − 1 > = l n x ) =\sum p_k (ln/ln2)(2^{-n_k}/p_k)<=\sum p_k(2^{-n_k}/p_k-1) (因爲x-1>=lnx) = ∑ p k ( l n / l n 2 ) ( 2 − n k / p k ) <= ∑ p k ( 2 − n k / p k − 1 ) ( 因爲 x − 1 >= l n x ) → 因爲∑ p k = 1 \sum p_k=1 ∑ p k = 1
= ( 1 / l n 2 ) ( − 1 + ∑ 2 − n k ) < = 0 =(1/ln2)(-1+\sum 2^{-n_k})<=0 = ( 1/ l n 2 ) ( − 1 + ∑ 2 − n k ) <= 0 結論:
H ( X ) < = n a v e H(\mathbb{X})<=n_{ave} H ( X ) <= n a v e 等號發生的條件:
1. ( 1 / p k ) ∗ 2 − n k = 1 也就是 n k = l o g ( 1 / p k ) 1. (1/p_k)*2^{-n_k}=1 也就是n_k=log(1/p_k) 1. ( 1/ p k ) ∗ 2 − n k = 1 也就是 n k = l o g ( 1/ p k ) 另外 UD 成立:
2. ∑ 2 − n k = 1 2.\sum 2^{-n_k}=1 2. ∑ 2 − n k = 1 結果:對於一個編碼要是能做到碼率逼近 H,那: 小的p k p_k p k n k n_k n k
經過以上結論,就可以通過 p 或者 n 來構建 haffman 編碼所需的 Binary Tree.
構建過程略;
在一個2 n 2^n 2 n
每一次將消耗2 n m a x − n k 2^{n_{max}-n_k} 2 n ma x − n k
∑ k 2 n m a x − n k < = 2 n m a x \sum _k 2^{n_{max}-n_k} <= 2^{n_{max}} k ∑ 2 n ma x − n k <= 2 n ma x haffman 編碼是 uniquely decodable . 這樣的很明顯的 coding 稱爲 instaneous (can immediate decode):每個a n a_n a n
以下再示範二者區別: 兩種編碼都是 UD: ∑ 2 − n k < = 1 \sum 2^{-n_k}<=1 ∑ 2 − n k <= 1
source instaneous non-instaneous a1 1 0 a2 01 01 a3 001 011 a4 0001 0111
很明顯 instaneous 的性質是順序讀取時可以立馬 decode。decoded code 可以連續存在互不干擾。
綜上,ID 是 UD 的 special case.通過∑ 2 − n k < = 1 \sum 2^{-n_k}<=1 ∑ 2 − n k <= 1
l o g ( 1 / p k ) log(1/p_k) l o g ( 1/ p k ) naive idea: use n k = [ l o g ( 1 / p N ) ] 取上整數 n_k = [log(1/p_N)]取上整數 n k = [ l o g ( 1/ p N )] 取上整數
n a v e = ∑ p k n K < ∑ p k ( l o g ( 1 / p k ) + 1 ) = H ( X ) + 1 n_{ave}=\sum p_kn_K<\sum p_k(log(1/p_k)+1)=H(\mathbb{X})+1 n a v e = ∑ p k n K < ∑ p k ( l o g ( 1/ p k ) + 1 ) = H ( X ) + 1 用 block coding 思路: 對於X n \mathbb{X^n} X n H ( X ) + 1 / n H(\mathbb{X})+1/n H ( X ) + 1/ n
一個性質: n a v e n_{ave} n a v e
claim:
p 1 > = p 2 > = p 3... > = p n p1>=p2>=p3...>=pn p 1 >= p 2 >= p 3... >= p n n 1 < = n 2 < = . . . < = n k n1<=n2<=...<=nk n 1 <= n 2 <= ... <= nk claim: n k − 1 = n k n_{k-1}=n_k n k − 1 = n k
因此誕生算法:嘗試將最長的兩個長度相等的 source code 移動到相等 level。可以首先給他們一個 common prefix,然後用 1 和 0 分開。再 merging。這個算法縮寫叫 HC: haffman coding.
haffman 的思路即從最小 p 的 a 出發,由下往上構建 Binary tree.
haffman 所做的:
找兩個最小 p 的 a。
通過H C ( p 1 , p 2 . . . p k − 2 , p k − 1 + p k ) HC(p_1,p_2...p_{k-2},p_{k-1}+p_k) H C ( p 1 , p 2 ... p k − 2 , p k − 1 + p k )
變成v ( b 1 ) , v ( b 2 ) , . . . . v ( b k − 1 ) v(b1),v(b2),....v(b_{k-1}) v ( b 1 ) , v ( b 2 ) , .... v ( b k − 1 )
v(ai)=v(bi)
v(ak-1)=v(bk-1) combine “0”
v(ak)=v(bk-1) combine “1”
*What if “many” of all are slightly wrongly coded?
for an example of X = 1 , 2 , 3 , . . . , 100 X={1,2,3,...,100} X = 1 , 2 , 3 , ... , 100 Y = 5 , 10 , 15 , . . . , 95 → H 0 = l o g 19 Y={5,10,15,...,95} → H0=log19 Y = 5 , 10 , 15 , ... , 95 → H 0 = l o g 19
that Y ⊆ X Y\sube X Y ⊆ X distortion : d(x,y) between X and Y ?
We set this measuring procedure as quantization .(reminds of JPEG??)
There’s two attribute of quantization , rate: |Y| and distortion :d(x,y)=(x-y)^2
e.g. X=6 , Y=5
其中一種可能編碼,這種編碼抛棄 2,3,6.如果 X 中出現 2,3,6 則會在編碼中損失。
\mbox 1 3 5 1 2 3 4 5 6 [ 1 1 1 1 1 1 ] d e t e r m i n i s t i c q u a n t i z a t i o n \begin{array}{lc} \mbox{}& \begin{array}{cc}1& 3 &5\end{array}\\ \begin{array}{c}1\\2\\3\\4\\5\\6\end{array}& \left[\begin{array}{cc} 1&\\ &1\\ &1\\ &&1\\ &&1\\ &&1\\ \end{array}\right] \end{array} ~~deterministic ~~~quantization \mbox 1 2 3 4 5 6 1 3 5 ⎣ ⎡ 1 1 1 1 1 1 ⎦ ⎤ d e t er mini s t i c q u an t i z a t i o n 在 Y 中: 1 出現概率 p1,3 出現 p2+p3,5 出現 p4+p5+p6,pi 是 X 中的各個概率
d ^ = p 2 + p 3 + p 6 \hat d=p_2+p_3+p_6 d ^ = p 2 + p 3 + p 6 另一種從 X 到 Y 的編碼,這次是概率隨機分配。(這種叫scalar quantization )
\mbox 1 2 3 4 5 6 1 3 5 [ 1 1 / 2 1 / 2 1 / 2 1 / 2 1 / 2 1 / 2 ] r a n d o m i z e d − q u a n t i z a t i o n 這圖需要修復 \begin{array}{lc} \mbox{}& \begin{array}{cc}1&2& 3&4 &5&6\end{array}\\ \begin{array}{c}1\\3\\5\end{array}& \left[\begin{array}{cc} 1&1/2&&&&&\\ &1/2&1/2\\ &&&1/2&1/2&1/2 \end{array}\right] \end{array} randomized-quantization 這圖需要修復 \mbox 1 3 5 1 2 3 4 5 6 ⎣ ⎡ 1 1/2 1/2 1/2 1/2 1/2 1/2 ⎦ ⎤ r an d o mi ze d − q u an t i z a t i o n 這圖需要修復 這裏 1 出現概率 p1+1/2p2,3 出現 1/2p2+p3+1/2p4 , 5 出現 1/2p4+p5+p6
d ^ = ∑ p ( x ) p ( y ∣ x ) d ( x , y ) \hat d=\sum p(x)p(y|x) d(x,y) d ^ = ∑ p ( x ) p ( y ∣ x ) d ( x , y ) 目標就是找到一個Y q Y_q Y q
r a t e : m i n − > r q = H ( Y q ) rate:min ->r_q=H(Y_q) r a t e : min − > r q = H ( Y q ) 有:
d ^ q = ∑ x , y p ( x ) q ( y ∣ x ) d ( x , y ) ≤ i n s t a n c e \hat d_q=\sum _{x,y}p(x)q(y|x)d(x,y)\le instance d ^ q = x , y ∑ p ( x ) q ( y ∣ x ) d ( x , y ) ≤ in s t an ce e.g.2
如果 X=1=Y
其中編碼時候 1 有δ \delta δ
r δ = H ( ( 1 + δ ) / 2 ) r_\delta=H((1+\delta)/2) r δ = H (( 1 + δ ) /2 ) d ^ δ = 1 / 2 ∗ δ \hat d_\delta =1/2*\delta d ^ δ = 1/2 ∗ δ 説明 randomized quantization 裏 d ^ \hat d d ^
在考慮 1 有δ 1 \delta_1 δ 1
d ^ = 1 / 2 ( δ + δ 1 ) \hat d=1/2(\delta+\delta_1) d ^ = 1/2 ( δ + δ 1 ) r = H ( ( 1 + δ − δ 1 ) / 2 ) r=H((1+\delta-\delta_1)/2) r = H (( 1 + δ − δ 1 ) /2 ) 利用block(vector)quantization 可以在差不多的 rate 下面得到低的 distortion:
X 3 → 000 , 111 X^3 →{000,111} X 3 → 000 , 111
可以讓x ∈ X 3 x\in X^3 x ∈ X 3
*vector distortion
d ( x ‾ , y ‾ ) = 1 / N ∑ n = 1 N d ( x n , y n ) , x , y ∈ X N d(\underline x,\underline y)=1/N\sum_{n=1}^N d(x_n,y_n),x,y\in X^N d ( x , y ) = 1/ N n = 1 ∑ N d ( x n , y n ) , x , y ∈ X N 那麽透過 vector distortion 能做到多好?
對於一個 X=1,Px=0,編碼到 Y,0 有 1/2 概率編碼成 1,1/2 變成 0,而 1 不出現。那:
typical y ∈ Y n \in Y^n ∈ Y n
這樣以來 對於給定的 x ,其 transition uncertainty:
∑ x q ( y ∣ x ) l o g ( 1 / p ( y ∣ x ) ) : t r a n s i t i o n U n v e r t a i n t y \sum_x q(y|x)log(1/p(y|x)):transition Unvertainty x ∑ q ( y ∣ x ) l o g ( 1/ p ( y ∣ x )) : t r an s i t i o n U n v er t ain t y 下面定義 Conditional entropy:
∑ x p ( x ) ∑ x q ( y ∣ x ) l o g ( 1 / p ( y ∣ x ) ) = H ( Y ∣ X ) ( c o n d i t i n a l E n t r o p y ) \sum_xp(x)\sum_x q(y|x)log(1/p(y|x))=H(\mathbb{Y|\mathbb{X}})(conditinal Entropy) x ∑ p ( x ) x ∑ q ( y ∣ x ) l o g ( 1/ p ( y ∣ x )) = H ( Y∣X ) ( co n d i t ina lE n t ro p y ) 真正的 uncertainty 是 H(Y)-H(Y|X).
另外知道 joint ensemble entropy:
H ( X , Y ) = ∑ x , y p ( x , y ) l o g ( 1 / p ( x , y ) ) H(X,Y)=\sum_{x,y}p(x,y)log(1/p(x,y)) H ( X , Y ) = x , y ∑ p ( x , y ) l o g ( 1/ p ( x , y )) →
H ( X ) = ∑ x ∑ y p ( x , y ) l o g ( 1 / p ( x ) ) H(X)=\sum_x\sum_yp(x,y)log(1/p(x)) H ( X ) = x ∑ y ∑ p ( x , y ) l o g ( 1/ p ( x )) H ( Y ) = ∑ x ∑ y p ( x , y ) l o g ( 1 / p ( y ) ) H(Y)=\sum_x\sum_yp(x,y)log(1/p(y)) H ( Y ) = x ∑ y ∑ p ( x , y ) l o g ( 1/ p ( y )) H ( Y ∣ X ) = ∑ x , y p ( x , y ) l o g ( 1 / p ( y ∣ x ) ) H(Y|X)=\sum_{x,y}p(x,y)log(1/p(y|x)) H ( Y ∣ X ) = x , y ∑ p ( x , y ) l o g ( 1/ p ( y ∣ x )) →
= ∑ x , y p ( x , y ) l o g ( p ( y ) / p ( x , y ) ) = H ( X , Y ) − H ( Y ) =\sum_{x,y}p(x,y)log(p(y)/p(x,y))=H(X,Y)-H(Y) = x , y ∑ p ( x , y ) l o g ( p ( y ) / p ( x , y )) = H ( X , Y ) − H ( Y ) 相似地:
H ( Y ∣ X ) = H ( X , Y ) − H ( X ) H(Y|X)=H(X,Y)-H(X) H ( Y ∣ X ) = H ( X , Y ) − H ( X ) hint: H(Y|X)=H(Y) given X.
現在再考慮 H(Y)-H(Y|X)=
∑ x , y p ( x , y ) l o g ( p ( y ∣ x ) / p ( y ) ) = ∑ p ( x , y ) l o g ( p ( x , y ) / p ( y ) p ( x ) ) = I ( X ; Y ) \sum_{x,y}p(x,y)log(p(y|x)/p(y))=\sum p(x,y)log(p(x,y)/p(y)p(x))=I(X;Y) x , y ∑ p ( x , y ) l o g ( p ( y ∣ x ) / p ( y )) = ∑ p ( x , y ) l o g ( p ( x , y ) / p ( y ) p ( x )) = I ( X ; Y ) 上式記作: Mutual Information ,注意中間式子裏 x,y 的對稱性。
n.d. 如果 x,y 是獨立事件,p(x,y)=p(x)p(y),那麽 log 裏的東西是 1,log1=0,I(X;Y)=0.即 X,Y 之間無 mutual Info.
↑ The whole graph represents H(X,Y)
我們同樣也可以得出:
0 ≤ I ( X , Y ) = H ( Y ) − H ( Y ∣ X ) ≤ H ( Y ) 0\le I(X,Y)=H(Y)-H(Y|X)\le H(Y) 0 ≤ I ( X , Y ) = H ( Y ) − H ( Y ∣ X ) ≤ H ( Y ) 繼續看:
∑ p ( x , y ) l o g ( p ( x , y ) / p ( y ) p ( x ) ) = I ( X ; Y ) \sum p(x,y)log(p(x,y)/p(y)p(x))=I(X;Y) ∑ p ( x , y ) l o g ( p ( x , y ) / p ( y ) p ( x )) = I ( X ; Y ) 上下翻轉 log 内容:
− I ≤ 1 / l n 2 ∑ p ( x , y ) [ p ( x ) p ( y ) / p ( x , y ) − 1 ] ( 不等式 x ≥ 1 − l n x ) -I\le1/ln^2\sum p(x,y)[p(x)p(y)/p(x,y)-1](不等式x\ge1-lnx) − I ≤ 1/ l n 2 ∑ p ( x , y ) [ p ( x ) p ( y ) / p ( x , y ) − 1 ] ( 不等式 x ≥ 1 − l n x ) 又
∑ p ( x , y ) [ p ( x ) p ( y ) / p ( x , y ) − 1 ] = 1 − 1 = 0 \sum p(x,y)[p(x)p(y)/p(x,y)-1]=1-1=0 ∑ p ( x , y ) [ p ( x ) p ( y ) / p ( x , y ) − 1 ] = 1 − 1 = 0 →
I ( X ; Y ) ≥ 0 I(X;Y)\ge0 I ( X ; Y ) ≥ 0 *typical x in X^n : p ( x ) ≈ 2 − N H ( X ) p(x)\approx2^{-NH(X)} p ( x ) ≈ 2 − N H ( X )
*typical y in Y^n : p ( y ) ≈ 2 − N H ( Y ) p(y)\approx2^{-NH(Y)} p ( y ) ≈ 2 − N H ( Y )
→typical (x,y) in (X*Y)^n: p ( x ‾ , y ‾ ) ≈ 2 − N H ( X , Y ) p(\underline x,\underline y)\approx 2^{-NH(X,Y)} p ( x , y ) ≈ 2 − N H ( X , Y )
如果上面三個條件都滿足,可以說是 jointly typical (x,y) in X,Y.
→
p ( x ) p ( y ) / p ( x ‾ , y ‾ ) = 2 − N ( H ( X ) + H ( Y ) − H ( X , Y ) ) = 2 − N I ( X ; Y ) ( K i n d O f U n c e r t a i n t y B e t w e e n X a n d Y ) p(x)p(y)/p(\underline x,\underline y)=2^{-N(H(X)+H(Y)-H(X,Y))}=2^{-NI(X;Y)} (KindOfUncertaintyBetweenXandY) p ( x ) p ( y ) / p ( x , y ) = 2 − N ( H ( X ) + H ( Y ) − H ( X , Y )) = 2 − N I ( X ; Y ) ( K in d O f U n cer t ain t y B e tw ee n X an d Y ) →
∑ i l o g ( p ( x i ) p ( y i ) / p ( x i , y i ) ) − > I ( X ; Y ) \sum_ilog (p(x_i)p(y_i)/p(x_i,y_i))->I(X;Y) i ∑ l o g ( p ( x i ) p ( y i ) / p ( x i , y i )) − > I ( X ; Y ) 總結,對於從 X 到 Y 的 encoding,考慮誕生的(x,y),從數量來説(x,y)的縂概率要是2 N ( H ( X ) + H ( Y ) ) 2^{N(H(X)+H(Y))} 2 N ( H ( X ) + H ( Y ))
但是實際上 Y 的情況和 X 据有關連,一個 typical x 出現對一個特定 y 的出現有影響。因此 typical (x,y)是2 ( N H ( X , Y ) ) 2^(NH(X,Y)) 2 ( N H ( X , Y ))
請注意 H(X)*H(Y)≥ \ge ≥
2 N H ( X , Y ) / 2 N ( H ( X ) + H ( Y ) ) = 1 / 2 N I ( X ; Y ) 2^{NH(X,Y)}/2^{N(H(X)+H(Y))}=1/2^{NI(X;Y)} 2 N H ( X , Y ) / 2 N ( H ( X ) + H ( Y )) = 1/ 2 N I ( X ; Y ) 所以説 I 表現了 X,Y 的一種相關程度,也就是我們能“掌握”X,Y 相關度,也就是編碼時的 certainty 衡量所需要的信息量。
*per symbol quantization scheme q(y|x):
for a distortion d(x,y):
d ^ q = ∑ x p ( x ) ∑ y q ( y ∣ x ) d ( x , y ) \hat d_q=\sum_xp(x)\sum_yq(y|x)d(x,y) d ^ q = x ∑ p ( x ) y ∑ q ( y ∣ x ) d ( x , y ) the formula above defines average distortion of x→y
Now consider an ensemble X-q>Y, q(y)=∑ x q ( y ∣ x ) p ( x ) \sum_x q(y|x)p(x) ∑ x q ( y ∣ x ) p ( x )
也就是 X,quantify 到 Y,其中的概率。根據之前的理論:
I g ( X ; Y ) = ∑ x ∑ y q ( y ∣ x ) l o g p ( x ) q ( y ∣ x ) p ( x ) q ( y ) I_g(X;Y)=\sum_x\sum_y q(y|x)log\frac{p(x)q(y|x)}{p(x)q(y)} I g ( X ; Y ) = x ∑ y ∑ q ( y ∣ x ) l o g p ( x ) q ( y ) p ( x ) q ( y ∣ x ) 其中一個結論是,當要做 X→Y,如果用 scale quantization, 根據最前面的理論要花費 H(Y),但是現在可以從所有 quantization 裏找到一個,使得I q ( X ; Y ) I_q(X;Y) I q ( X ; Y ) d ^ q ≤ D \hat d_q\le D d ^ q ≤ D I q I_q I q I q I_q I q
這個小 q 是個 scale quantization
該圖叫 rate-distortion curve, 描述 VQ Scheme
上圖的紅綫表示各種 q,綠色表示最小的 q,形狀反映了 d 越大 rate 越小,他們是此消彼長的。
Rate 的完全定義是:
R ( D ) = m i n V Q l o g X N : s . t . d V Q ≤ D R(D)=min_{VQ} \frac{logX}{N} :s.t. d_{VQ}\le D R ( D ) = mi n V Q N l o g X : s . t . d V Q ≤ D 就是對於 D, D 是一個我們接受的可以 will show 的程度,能做到的最小 rate。我們找到最小的I I I
*rate-distortion theorem:
given X , p , Y , d ( x , y ) , D X,p,Y,d(x,y),D X , p , Y , d ( x , y ) , D
if R I ( D ) = R R_I(D)=R R I ( D ) = R
R I ( D ) = m i n q : d ˉ q ≤ D I ( X ; Y ) = R R_I(D)=min_{q:\bar d_q\le D} I(X;Y)=R R I ( D ) = mi n q : d ˉ q ≤ D I ( X ; Y ) = R then exists VQ scheme with M ≤ 2 ( R + e ) N M\le2^{(R+e)N} M ≤ 2 ( R + e ) N d ^ V Q ≤ D + e \hat d_{VQ}\le D+e d ^ V Q ≤ D + e
這個 M 就是對應的 Codewords:|C|= ∣ μ ( X n ) ∣ |\mu(X^n)| ∣ μ ( X n ) ∣
→
R V Q = ( R + e ) N N R_{VQ}=\frac{(R+e)N}{N} R V Q = N ( R + e ) N (上面的 VQ scheme 需要有 on length-N vector for N large enough ,也就是把 N 的 向量 x 變成向量 y,兩個向量分別屬於 X,Y
這裏判定依然用d ( x , y ) = 1 N ∑ n d ( x n , y n ) d(\mathbb{x},y)=\frac{1}{N}\sum_n d(x_n,y_n) d ( x , y ) = N 1 ∑ n d ( x n , y n )
(在上面的 d*VQ,就是我們證明中假定d ^ ∗ V Q = R _ ( V ) \hat d*{VQ}=R\_{(V)} d ^ ∗ V Q = R _ ( V )
→
thus:
R ( V ) ( D + e ) ≤ R ( I ) ( D ) + e R_{(V)}(D+e)\le R_{(I)}(D)+e R ( V ) ( D + e ) ≤ R ( I ) ( D ) + e
接下來仔細研究 vector quantization,即從 x 變成 y 的情況, 一般總有一個最佳匹配使我們有最棒的 D-R 曲綫。這個的策略會是“Min distance”,
那麽我們應該關注 X 中的 x 的 typical 的情況,我們知道它的概率是2 − 2 N H ( X ) 2^{-2NH(X)} 2 − 2 N H ( X )
總結:
選擇的映射應該有最小的 distortion. v ( x ) = m i n c m d ( x , C m ) v(x)=min_{c_m} d(x,C_m) v ( x ) = mi n c m d ( x , C m ) 對於編碼,要把 typical 的 x 做好 only care about typical . 目標就是
d ( x , v ( x ) ) ( t y p i c a l ) ≤ D + 1 2 e ( f o r E v e r y T y p i c a l ( x ) d(x,v(x)) (typical )\le D+\frac{1}{2}e (forEveryTypical (x) d ( x , v ( x )) ( t y p i c a l ) ≤ D + 2 1 e ( f or E v ery T y p i c a l ( x ) 這裏的 1/2 改成任何小於 1 的分數都可以。
Lin 的思路是抓 typical 的 x 放給 typical 的 y,typical 的 x 有2 N H ( X ) 2^{NH(X)} 2 N H ( X )
如果只抓 typical,那麽最後會得到
d ^ ( t y p i c a l x , t y p i c a l y ) ≤ D + k e , 0 < k < 1 \hat d(typical x,typicaly)\le D+ke,0<k<1 d ^ ( t y p i c a l x , t y p i c a l y ) ≤ D + k e , 0 < k < 1 但是問題是,typical 有 2 N H ( X ) 2^{NH(X)} 2 N H ( X )
方法一 : Typical First
我們需要從 X 和 Y 共同的關係出發,定義 T(x,y):
T ( x , y ) = { ( x , y ) : p ( x , y ) ≈ 2 − N H ( X , Y ) } T_{(x,y)}=\{(x,y):p(x,y)\approx2^{-NH(X,Y)}\} T ( x , y ) = {( x , y ) : p ( x , y ) ≈ 2 − N H ( X , Y ) } 這裏 Y 是一個我們可以從中選出 codewords 的集合,x,y 均是向量(因爲在討論 VQ),并非 Y 就是編碼好的 codewords assemble
把上面的式子變化一下,依然要求滿足d ˉ ≤ D + e \bar d\le D+e d ˉ ≤ D + e
∣ 1 N l o g 1 p ( x , y ) − H ( X , Y ) ∣ ≤ e |\frac{1}{N}log\frac{1}{p(x,y)}-H(X,Y)|\le e ∣ N 1 l o g p ( x , y ) 1 − H ( X , Y ) ∣ ≤ e ∣ 1 N l o g 1 p ( x ) − H ( X ) ∣ ≤ e |\frac{1}{N}log\frac{1}{p(x)}-H(X)|\le e ∣ N 1 l o g p ( x ) 1 − H ( X ) ∣ ≤ e ∣ 1 N l o g 1 p ( y ) − H ( Y ) ∣ ≤ e |\frac{1}{N}log\frac{1}{p(y)}-H(Y)|\le e ∣ N 1 l o g p ( y ) 1 − H ( Y ) ∣ ≤ e 上式的形式都是 S a m p l e ‘ s e n t r o p y − E x c e p t i o n < = e : _Sample‘s entropy -Exception<= e_: S am pl e ‘ se n t ro p y − E x ce pt i o n <= e :
∣ 1 c o d e l e n g t h H ( s a m p l e ) − E n t r o p y ∣ = ∣ C o d e R a t e − E n t r o p y ∣ ≤ e |\frac{1}{codelength} H(sample)-Entropy|=|CodeRate-Entropy|\le e ∣ co d e l e n g t h 1 H ( s am pl e ) − E n t ro p y ∣ = ∣ C o d e R a t e − E n t ro p y ∣ ≤ e 以上的條件滿足的( x,y)(均為向量)就成爲了 jointly typical :
1 N l o g p ( x , y ) p ( x ) p ( y ) − I ( X ; Y ) ≤ 3 e \frac{1}{N}log\frac{p(x,y)}{p(x)p(y)}-I(X;Y)\le 3e N 1 l o g p ( x ) p ( y ) p ( x , y ) − I ( X ; Y ) ≤ 3 e 記:
i ( x , y ) = 1 N l o g p ( x , y ) p ( x ) p ( y ) i(x,y)=\frac{1}{N}log\frac{p(x,y)}{p(x)p(y)} i ( x , y ) = N 1 l o g p ( x ) p ( y ) p ( x , y ) jointly typical 在數學上説明它和 I(X;Y)不會差太大
(x,y)要成爲 jointly typical,既要滿足 x 是 typical,y 是 typical,還要滿足 x,y 這對組合的出現也是 typical 的。
它的關係度是低於等於 I(X;Y)
如果(x,y)還能滿足:
∣ 1 N ∑ d ( x n , y n ) − d ˉ q ∣ ≤ e |\frac{1}{N}\sum d(x_n,y_n)-\bar d_q|\le e ∣ N 1 ∑ d ( x n , y n ) − d ˉ q ∣ ≤ e 則它還是 distortion typical
由此定義出 T:
T : { ( x , y ) ∣ i ( x , y ) − I ( X ; Y ) ≤ e , d ( x , y ) − d ˉ q ≤ e } T:\{(x,y)|i(x,y)-I(X;Y)\le e,d(x,y)-\bar d_q\le e\} T : {( x , y ) ∣ i ( x , y ) − I ( X ; Y ) ≤ e , d ( x , y ) − d ˉ q ≤ e } 方法二 From Codebook
想找幾個在 Y^n 中的 c,它們是 distortion typical y. 它們滿足 distortion typical. 上面已經說了這樣的 c 一共有 M 個
然後再從 X^n 中挑選 x 去匹配。
問題是如何找到這個C \mathbb{C} C
*a “randomized algorithm” for “constracting” C \mathbb{C} C
C → ( p ( y ) M \mathbb{C} →(p(y)^M C → ( p ( y ) M x 1 x_1 x 1
如果 M 次都沒有匹配到(p a y > d ˉ q + e pay>\bar d_q+e p a y > d ˉ q + e ( 1 − P T ( x 1 ) ( y ) ) M , P T ( x 1 ) ( y ) = ∑ y ∈ T ( x 1 ) p ( y ) (1-P_{T(x_1)}(y))^M,P_{T(x_1)}(y)=\sum_{y\in T(x_1)}p(y) ( 1 − P T ( x 1 ) ( y ) ) M , P T ( x 1 ) ( y ) = ∑ y ∈ T ( x 1 ) p ( y )
補充:這個意思是對於一組特定的 codebook,讓 x1 找不到裏面有合適的 c 的概率。
要讓這個概率足夠小,1-XX 的 XX 部分足夠大:
因爲:
1 N l o g p ( x , y ) p ( x ) p ( y ) − I ( X ; Y ) ≤ e \frac{1}{N}log\frac{p(x,y)}{p(x)p(y)}-I(X;Y)\le e N 1 l o g p ( x ) p ( y ) p ( x , y ) − I ( X ; Y ) ≤ e p ( x , y ) p ( x ) = p ( y ∣ x ) \frac{p(x,y)}{p(x)}=p(y|x) p ( x ) p ( x , y ) = p ( y ∣ x ) 所以:
∑ y ∈ T ( x 1 ) p ( y ) ≥ ∑ y ∈ T ( x 1 ) p ( y ∣ x ) × 2 − ( I + e ) N \sum_{y\in T(x_1)}p(y)\ge \sum_{y\in T(x_1)}p(y|x)\times 2^{-(I+e)N} y ∈ T ( x 1 ) ∑ p ( y ) ≥ y ∈ T ( x 1 ) ∑ p ( y ∣ x ) × 2 − ( I + e ) N 這裏
∑ y ∈ T ( x 1 ) p ( y ∣ x ) ≈ 1 ( t r i c k y ) \sum_{y\in T(x_1)}p(y|x) \approx 1 ~~~(tricky) y ∈ T ( x 1 ) ∑ p ( y ∣ x ) ≈ 1 ( t r i c k y ) 對於 ( 1 − P T ( x 1 ) ( y ) ) M (1-P_{T(x_1)}(y))^M ( 1 − P T ( x 1 ) ( y ) ) M
= e M l n ( 1 − P T ( x 1 ) ( y ) ) ≤ e M ( 1 − P T ( x 1 ) ( y ) − 1 ) = e − 2 ( R + e ) N 2 P T ( x 1 ) ( y ) = e − 2 e N =e^{Mln(1-P_{T(x_1)}(y))}\le e^{M(1-P_{T(x_1)}(y)-1)}=e^{-2^{(R+e)N}2^{P_{T(x_1)}(y)}}=e^{-2^{eN}} = e Ml n ( 1 − P T ( x 1 ) ( y )) ≤ e M ( 1 − P T ( x 1 ) ( y ) − 1 ) = e − 2 ( R + e ) N 2 P T ( x 1 ) ( y ) = e − 2 e N thus:
( 1 − P T ( x 1 ) ( y ) ) M + a t y p i c a l ≤ d 大 ≤ e (1-P_{T(x_1)}(y))^M+atypical \le d_大\le e ( 1 − P T ( x 1 ) ( y ) ) M + a t y p i c a l ≤ d 大 ≤ e *How many bits to represent X \mathbb{X} X H o ( X ) H_o(X) H o ( X )
[compression]*How many bits to represent X^n with error δ \delta δ N H ( X ) NH(X) N H ( X )
[compression]*How many bits to represent X with error δ \delta δ H ( X ) H(X) H ( X )
[+quantization]*How many bits to represen t X^n with fixed-length codewords with ≤ D \le D ≤ D N R I ( D ) = N × m i n q I ( X q ; Y q ) NR_I(D)=N\times min_qI(X_q;Y_q) N R I ( D ) = N × mi n q I ( X q ; Y q )
*How many bits to transmit X^n with ≤ ϵ \le \epsilon ≤ ϵ Through “Known” noise p (y|x) )?
Shannon’s Second Theory
在這個問題,可以推測出結果的上限是一個 < ≈ N ∗ C <\approx N*C <≈ N ∗ C C = m a x q I ( X ; Y ) C=max_qI(X;Y) C = ma x q I ( X ; Y )
X = 1 , 2 , 3 , . . . , K , Y = 1 , 2 , 3 , . . . , J X={1,2,3,...,K} , Y={1,2,3,...,J} X = 1 , 2 , 3 , ... , K , Y = 1 , 2 , 3 , ... , J
對於 noise(error) : p(y|x),很容易理解它形成一個 probability transmit matrix,這裏記作 Channel
計算 error 的方法: 考慮X − ν > Y − μ > X ^ X-\nu>Y-\mu>\hat X X − ν > Y − μ > X ^ E p ( y ∣ x ) [ [ x ≠ μ ( y ) ] ] E_{p(y|x)}[[x\ne \mu(y)]] E p ( y ∣ x ) [[ x = μ ( y )]]
worst-case : error=m a x x E p ( y ∣ x ) [ [ x ≠ μ ( y ) ] ] max_x E_{p(y|x)}[[x\ne\mu(y)]] ma x x E p ( y ∣ x ) [[ x = μ ( y )]]
説明 x 不能全部選來自 X 的,應該是 x ‾ ∈ c o d e b l o c k s ⊂ X n \underline x\in codeblocks \subset \mathbb{X}^n x ∈ co d e b l oc k s ⊂ X n
“safe” transmission:
transmit only { x 1 , x 2 , . . . , x M } \{x_1,x_2,...,x_M\} { x 1 , x 2 , ... , x M } P E x ‾ m ≤ ϵ P_E^{\underline x_m} \le \epsilon P E x m ≤ ϵ
上面的意思是說,如果我們傳送 all x in X, 导致 channel 的使用率過大。 我們可以在e r r o r < e error<e error < e x ˉ \bar x x ˉ X n X^n X n x ˉ \bar x x ˉ
Q: What is maximum l o g M N \frac{log M}{N} N l o g M
A: ≈ \approx ≈ I ( X ˉ q ; Y ˉ q ) I(\bar X_q;\bar Y_q) I ( X ˉ q ; Y ˉ q )
這個 C 就是一開始我們預測的 C, Channel Capacity.
傳送的 X 是 n 個 unit, 取 M 個 Codewords 去 transmit。C=l o g M N \frac{logM}{N} N l o g M μ \mu μ
Codewords 肯定是會分散在 X^n 裏。
given 0 < R < C 0<R<C 0 < R < C ϵ > 0 \epsilon >0 ϵ > 0
that exists a protocol that archieves rate l o g M / N > = R logM/N >= R l o g M / N >= R
and error max_m P E c ‾ m ≤ ϵ P_E^{\underline c_m} \le \epsilon P E c m ≤ ϵ
assume q(x) that achieves C \mathbf{C} C
construct C \mathbf{C} C p ( x ˉ ) p(\bar x) p ( x ˉ )
μ ( y ) = c ‾ \mu(y)=\underline c μ ( y ) = c ( c ‾ , y ‾ ) (\underline c, \underline y) ( c , y )
ν ( x ‾ ) = c ‾ \nu(\underline x)=\underline c ν ( x ) = c d ( x ‾ , c ‾ ) d(\underline x,\underline c) d ( x , c )
underline x 和 x bar 疑似是一樣的
我們在這一章做的是,對於一個沒有概率問題需要考慮的 X^n,要通過 channel 來 transmit 成 Y^n.
那麽三個步驟是:
我們沒必要把每個 element in X^n,都丟給 channel。我們需要挑選一部分比較不容易出問題的 element,也就是構建 q(x),這部分我們挑出來的就稱作 codebook,他們構成一個建立在 channel 上抽象的 p(x,y)(這個實際上不存在)
那麽緊接著 1,這部分 x 要怎麽找出來呢? 我們丟 x 進 channel,然後看出來的哪些 y 再對應回來的 x 的情況,找到每個 q(x)(q(x)的意思就是取一部分 x in X),找其中表現最好的,也就是再對應回來的 x 和原來的 x 的 joint Information
完成 1 和 2 后,我們就可以推導出我們要的 encoder 和 decoder 的性質,也就是我們找到的 codewords 和 y 是 joint typical,而且我們的 x 和 c 的 distortion 是最小的。這樣就封閉了我們的理論。
注意整個有 M 個元素的的 Codebook,傳 N 長度的信息(channel 使用了 N 次),碼率是l o g M N \frac{logM}{N} N l o g M
在這個概念上注意最大的 capacity 是C = m a x I ( X q ; Y q ) C=maxI(X_q;Yq) C = ma x I ( X q ; Y q )
最終,目標是對於直接傳輸的 R,我們有: for any R < C R<C R < C C > r a t e ≥ R C>rate\ge R C > r a t e ≥ R
在物理上,Codebooks 做的事情是把比較容易受 noise 而混淆的 info 拉開成不易被 noise 干擾而混淆的 C 進行傳送,進而增大 distortion.
邊緣情況: 1. 不太 typical:會存在有拿到的 y 無法 decode。(如果 M 很大,這個可能性很小)
Typical : M不是很大也OK Back to last chapter. Let’s talk:
*How many bits to represent X = s 1 , s 2 , . . . s k X={s1,s2,...sk} X = s 1 , s 2 , ... s k s m ∈ { 0 , 1 } s_m\in \{0,1\} s m ∈ { 0 , 1 }
如果要存儲一個 zip 檔案:
S y m b o l t a b l e + H u f f m a n i n f o + e n c o d e d b i t s ≈ N H ( X ) Symbol~table+Huffman~info+encoded~bits\approx NH(X) S y mb o l t ab l e + H u ff man in f o + e n co d e d bi t s ≈ N H ( X ) *compression of binary string losslessly:
S − > ν ( S ) − > μ ( v ( S ) ) = S S->\nu(S)->\mu(v(S))=S S − > ν ( S ) − > μ ( v ( S )) = S ∈ { 0 , 1 } ( i n f i n i t e ) ∈ { 0 , 1 } ( i n f i n i t e ) ∈ { 0 , 1 } \in\{0,1\}(infinite)~~\in\{0,1\}(infinite)~~\in\{0,1\} ∈ { 0 , 1 } ( in f ini t e ) ∈ { 0 , 1 } ( in f ini t e ) ∈ { 0 , 1 } 目的是∣ v ( s ) ∣ < ∣ s ∣ |v(s)|<|s| ∣ v ( s ) ∣ < ∣ s ∣
但是概念上,∣ v ( s ) ∣ < ∣ S ∣ |v(s)|<|S| ∣ v ( s ) ∣ < ∣ S ∣
但是有些“easy”情況: 比方説 S = 0000...0 S= 0000...0 S = 0000...0 S = 01010101....01 S=01010101....01 S = 01010101....01 Programming easiness
with respect to an universal computing model U
K u ( S ) = m i n { ∣ P ∣ : U ( P ) = S } K_u(S)=min\{|P|:U(P)=S\} K u ( S ) = min { ∣ P ∣ : U ( P ) = S } 注意:这里的 K 值(柯氏复杂度)是基于 U 的。所以记 K_U, U 不一样,K 也不同。这里的 P 是 program,可以是一些不同的 Turing machine 之类。
An important feature of K-Complexity: Kolmogorov complexity is small relative to the string's size
Explain:
S is a binary string ∈ { 0 , 1 } \in \{0,1\} ∈ { 0 , 1 } requirement is we want the simplest program P.
*One of computing model is the Turing machine (Does not mean U can be M, but P can be M). Turing machine already defined "computable function”, which is a transition from INPUT to OUTPUT , with 3 possible procedure: Move forward, Move back, Write(in the time of tape) , which is a mechanical computing process that can halt .
Thus : f is a computable function , if there exists Turing Machine M such that M(x)=f(x) for all x.
As for Universal Computing Model U , for different machine, we can let M be like different programs for U :
U ( P f , x ) = f ( x ) U(P_f,x)=f(x) U ( P f , x ) = f ( x ) U is like a program simulator. P_f is "M” in U. (这些话的意思是 unify 各种 M 到 U 上,以及讨论用 code 可以把 data 压到多短)
warning↑ 这部分牵扯到 automata and stack machine 的内容。
“K U K_U K U c 2 c_2 c 2
K U 1 ( S ) ≤ K U 2 ( S ) + c 2 K_{U1}(S)\le K_{U2}(S)+c_2 K U 1 ( S ) ≤ K U 2 ( S ) + c 2 Define : P 2 P_2 P 2 U 2 U_2 U 2 U 1 U_1 U 1
P S P_S P S K U 2 K_{U_2} K U 2 U 2 U_2 U 2
then:
U 1 ( P 2 P s ) = U 2 ( P s ) = S U_1(P_2P_s)=U_2(P_s)=S U 1 ( P 2 P s ) = U 2 ( P s ) = S And within this equation:
P 2 − > ∣ P 2 ∣ , P s − > K U 2 ( S ) P_2->|P_2|,P_s->K_{U_2}(S) P 2 − > ∣ P 2 ∣ , P s − > K U 2 ( S ) 上面的意思是, 本来 S 是 U2 通过运行 Ps 产生的,现在用 U1 模拟运行 U2,且我们要付出额外代价,也可产生 S。
上面这句话会引出不变性定理:Invariance theorem:
不变性定理说:对于 S,有机会用一些最佳的程式 P 来运行,但是总要付出一个额外固定常数的代价,这个常数取决于 P 的类型(java、python、English,etc.)。
结论:存在 C2 大于等于 0:
− c 1 + K U 2 ( S ) ≤ K U 1 ( S ) ≤ K U 2 + c 2 -c_1+K_{U_2}(S)\le K_{U_1}(S)\le K_{U_2}+c_2 − c 1 + K U 2 ( S ) ≤ K U 1 ( S ) ≤ K U 2 + c 2 and
K ( S ) ≤ ∣ S ∣ + C ( “ i n p u t " + " c o p y " ) K(S)\le|S|+C (“input"+"copy") K ( S ) ≤ ∣ S ∣ + C ( “ in p u t " + " co p y " ) ∃ S , s u c h t h a t K ( S ) ≥ ∣ S ∣ \exist S, such~ that ~~K(S)\ge |S| ∃ S , s u c h t ha t K ( S ) ≥ ∣ S ∣ Back to the model:
S − ν > P − μ > S S-\nu>P-\mu>S S − ν > P − μ > S if ν \nu ν
→ short program for string with large K(s)
If K(S) computable → exist M for computing K(S).
假设有一个 Program M,它从短到长遍历全部可能的二进制序列。它输入一个复杂度 L,当它生成到的序列 K 复杂度大于 L 时立马停止,那它就能生成 K 复杂度大于 L 的最短序列。
那么它的输出 S 的 K 复杂度就是 L,是很大。但是它本身很小,这个 program 的 cost 可能是 C+|M|+LogL(本身环境消耗+算法消耗+迭代 L),这就产生了悖论:我们可以用 K 复杂度小于 L 的 M 来弄出 K 复杂度是 L 的 S————结论就是一开始 K(S)就不可计算。Not computable.
在数学上,能讓 K(S) computable 的 M 是没有的。
*Considering some P that achieves K(S) that takes a very very long time?
for a ensemble X:
X = { s 1 , s 2 . . . , s k } X=\{s_1,s_2...,s_k\} X = { s 1 , s 2 ... , s k } H ( X ) = ∑ k = 1 k p k l o g 1 p k (1) H(X)=\sum_{k=1}^k p_k log\frac{1}{p_k} \tag{1} H ( X ) = k = 1 ∑ k p k l o g p k 1 ( 1 ) Now we can define the formula of K(X) similarly:
K ( X ) = ∑ k = 1 k p k × K ( S k ) (2) K(X)=\sum_{k=1}^kp_k\times K(S_k) \tag{2} K ( X ) = k = 1 ∑ k p k × K ( S k ) ( 2 ) 這裏(1)是統計上的靜態結果。(2)表示了一種在 Compute 過程中 not computable 的複雜度的關係。
A special case:
assume for :
X = B N = { s 1 , s 2 . . . s 2 N } X=B^N=\{s_1,s_2...s_{2^N}\} X = B N = { s 1 , s 2 ... s 2 N } and there is a s b s_b s b K ( S b ) ≥ N K(S_b)\ge N K ( S b ) ≥ N p ∗ s b = 1 p*{s_b}=1 p ∗ s b = 1
thus:
H ( X ) = 0 , K ( X ) ≥ N H(X)=0,K(X)\ge N H ( X ) = 0 , K ( X ) ≥ N This case is the "worst“ case,right?
Regular case:
回到定義所有長度 N 的 s 的 B,定義 B 的分佈: θ , 1 − θ → 1 , 0 {\theta,1-\theta}→{1,0} θ , 1 − θ → 1 , 0
那麽 p ( s ) = θ n ( 1 − θ ) N − n p(s)=\theta^n (1-\theta)^{N-n} p ( s ) = θ n ( 1 − θ ) N − n
→
H ( X ) = N H ( θ ) H(X)=N\mathcal{H}(\theta) H ( X ) = N H ( θ ) H ( θ ) = θ l o g 1 θ + ( 1 − θ ) l o g 1 1 − θ \mathcal{H}(\theta)=\theta log \frac{1}{\theta}+(1-\theta)log\frac{1}{1-\theta} H ( θ ) = θl o g θ 1 + ( 1 − θ ) l o g 1 − θ 1 Actually:
K ( X ) ≈ b y s h o r t − p r o g r a m m i n g H ( X ) ≈ b y b l o c k c o d i n g H δ ( X ) K(X)\approx_{by~short-programming} H(X)\approx_{by~block~coding} H_\delta(X) K ( X ) ≈ b y s h or t − p ro g r ammin g H ( X ) ≈ b y b l oc k co d in g H δ ( X ) Because in block coding, the entropy is mainly defined by(focus on) typical block
Thus, we can say that show typical ≈ \approx ≈
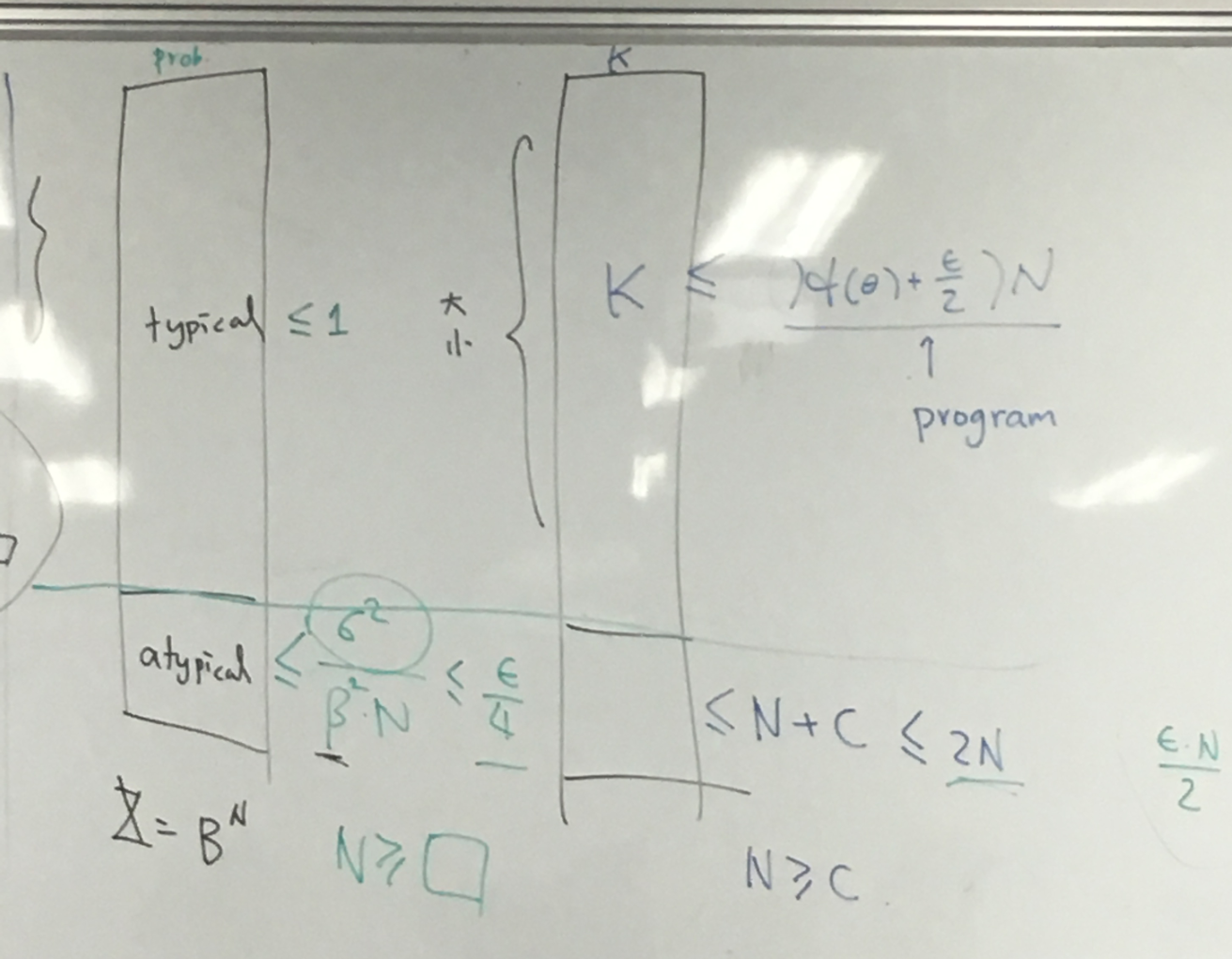
G i v e n ϵ > 0 , ∃ N 0 , s t . N ≥ N 0 → K ( X ) ≤ ( H ( θ ) + ϵ ) N Given~\epsilon >0,\exist N_0,st.N\ge N_0~~\rightarrow K(X)\le(\mathcal{H}(\theta)+\epsilon)N G i v e n ϵ > 0 , ∃ N 0 , s t . N ≥ N 0 → K ( X ) ≤ ( H ( θ ) + ϵ ) N Also:
( H ( θ ) − ϵ ) N ≤ K ( X ) ≤ ( H ( θ ) + ϵ ) N (\mathcal{H}(\theta)-\epsilon)N\le K(X)\le(\mathcal{H}(\theta)+\epsilon)N ( H ( θ ) − ϵ ) N ≤ K ( X ) ≤ ( H ( θ ) + ϵ ) N we can consider the range of atypical and typical H(X) and K(X) as the diagram above.
Notice that, we have to write a program to get all typical S:
And the cost is fixed program cost C, plus logN, plus Index ,which is the most highly connected to N.
This program , creates every possible s, and if the s is typical, then return the table with its index.
考慮幾個程序,對一個字串 010101010,的下一位進行預測。
它的預測可能是 0,可能是 1,可能是 0101010(halts here)。
對於 U(P)=x,若這個長度是 M 的程序 P 是用 fair random bit flip 的方式,那對任何可能的 x 的概率 p(x)
p ( x ) = ∑ P 1 2 M [ [ U ( P ) = x ] ] p(x)=\sum_P\frac{1}{2^M}[[U(P)=x]] p ( x ) = P ∑ 2 M 1 [[ U ( P ) = x ]] 那其實全部可能長度的程序 P 都是:
p ( x ) = ∑ m = 1 ∞ ∑ P 1 2 m [ [ U ( P ) = x ] ] p(x)=\sum_{m=1}^\infin\sum_P\frac{1}{2^m}[[U(P)=x]] p ( x ) = m = 1 ∑ ∞ P ∑ 2 m 1 [[ U ( P ) = x ]] 那麽得到的這個 p(x)就可能符合某種分佈。(有些特定的字串可能是有特定的程序產生,它的概率就低。簡單的字串可能很多程序都能打印出來,它的概率就高)
這個分佈可以叫做 Universal Distribution
回到一開始的問題,我們現在在比較:
p ( x t − 1 0 ) p(x_{t-1} 0) p ( x t − 1 0 ) p ( x t − 1 1 ) p(x_{t-1} 1) p ( x t − 1 1 ) 哪個大。也就是説程序預測下一位是 0 還是 1 哪個概率大。
*對於全部能生成從 1 到 M 字節長度的程式,按道理說,假設一個程式生成器(比如猴子敲鍵盤),它對於 N 字節長度能有 1/2^N 的可能性生成共 2^N 個程式。
但是我們不需要這樣平凡分散的情況。那有幾種解決辦法:
只保留“合法”的程式。(定義出合法的規則)(但是無法 guarantee on ∑ P r ( P ) \sum P_r(P) ∑ P r ( P )
有個問題是每種情況的可能性總數:∑ P r ( P ) \sum Pr(P) ∑ P r ( P ) ∑ P r ( P ) \sum Pr(P) ∑ P r ( P )
我們把每個程式的可能性:1 2 N \frac{1}{2^N} 2 N 1 1 4 N \frac{1}{4^N} 4 N 1
殘念,以上的情況都很少人有研究。
主流的解決方案:
Consider programs that are prefix-free (什麽是 prefix-free? huffman code 就是 prefix-free)
define ensemble : p ‾ {\underline p} p
0 < ∑ ∣ p ∣ o f p ‾ 2 − ∣ p ∣ ≤ 1 (Kraff’s Ineg) 0<\sum_{|p|~of~{\underline p}}2^{-|p|}\le1 \tag{Kraff's Ineg} 0 < ∣ p ∣ o f p ∑ 2 − ∣ p ∣ ≤ 1 ( Kraff’s Ineg ) 這個意思是,全部定字節長度的全部 prefix-free 的程式的概率肯定在 0 到 1 之間。
用這種規則定義出來的程式集合記作 prefix K-complexity aka prefix Chaitin-Complexity
而我們一開始定義的稱 plain K-complexity
類似 entropy 的:
H ( X ; Y ) = H ( X ) + H ( Y ∣ X ) H(X;Y)=H(X)+H(Y|X) H ( X ; Y ) = H ( X ) + H ( Y ∣ X ) 對於兩個 program,generate 出兩個 b string s, t ,也有
K c ( s , t ) ≈ K C ( s ) + K C ( t ∣ s ) K_c(s,t)\approx K_C(s)+K_C(t|s) K c ( s , t ) ≈ K C ( s ) + K C ( t ∣ s ) *Simple-string distribution(encode 了對計算簡單和計算困難的想象)
p ( s ‾ ) = ∑ p : U ( p ‾ ) = s ‾ 2 − ∣ p ‾ ∣ (1) p(\underline s)=\sum_{p:U(\underline p)=\underline s} 2^{-|\underline p|} \tag{1} p ( s ) = p : U ( p ) = s ∑ 2 − ∣ p ∣ ( 1 ) 描述一個 prefix 字符串 s 的概率。
對於計算困難,chaitin 説明了計算困難的 string 是找不到(很難找到)程式的。
*Chaitin's constant for any Program that can halt :
define
Ω F = ∑ p ∈ P F 2 − ∣ p ∣ \Omega_F=\sum_{p\in P_F}2^{-|p|} Ω F = p ∈ P F ∑ 2 − ∣ p ∣ 大概的解釋:http://www.matrix67.com/blog/archives/901
這個常數表示一個程式 halt 的概率,它是存在且可定義的,但是不可計算。
(1)是 predict 任意一個字串的概率。
*對於給的 t-1 個 bit 和下一個未知 bit x 組成的字串 s 1 s 2 s 3 … s t − 1 s x s_1s_2 s_3\dots s_{t-1} s_x s 1 s 2 s 3 … s t − 1 s x
定義
p x ( s ‾ ) = ∑ x ∈ β + ∪ { Λ } p ( s ‾ x ‾ ) p_x(\underline s)=\sum_{x\in \beta ^+ \cup \{\Lambda\}}p(\underline s \underline x) p x ( s ) = x ∈ β + ∪ { Λ } ∑ p ( s x ) p_x 就是得出一個字符串,前 t-1 個是固定的 bit 的概率。(beta+ \cup \lambda 指的是 0 和 1 的集合以及停止符。)
那麽有:
p x ( s t ∣ s t − 1 ‾ ) = p ( s ‾ x ) p x ( s x − 1 ) ‾ p_x(s_t|\underline {s_{t-1}})=\frac{p(\underline s_x)}{p_x(\underline{s_{x-1})}} p x ( s t ∣ s t − 1 ) = p x ( s x − 1 ) p ( s x ) p x ( λ ∣ s ‾ t − 1 ) = 1 − p x ( 1 ∣ s ‾ t − 1 ) − p x ( 0 ∣ s t − 1 ) p_x(\lambda|\underline s_{t-1})=1-p_x(1|\underline s_{t-1})-p_x(0|s_{t-1}) p x ( λ ∣ s t − 1 ) = 1 − p x ( 1∣ s t − 1 ) − p x ( 0∣ s t − 1 ) (定義 lambda 是下一個是停止符)上式的意思是下一個是停止符的概率是 1-p(下一個是 1)-p(下一個是 0)
定義我們做預測要付出的 error rate:
首先我們知道對於一個要預測的\hat s_t
p ( s ^ t = 1 ) = p x ( 1 ∣ s t − 1 ) p(\hat s_t=1)=p_x(1|s_{t-1}) p ( s ^ t = 1 ) = p x ( 1∣ s t − 1 ) p ( s ^ t = 0 ) = p x ( 0 ∣ s t − 1 ) p(\hat s_t=0)=p_x(0|s_{t-1}) p ( s ^ t = 0 ) = p x ( 0∣ s t − 1 ) p ( s ^ t = λ ) = p x ( λ ∣ s t − 1 ) p(\hat s_t=\lambda)=p_x(\lambda|s_{t-1}) p ( s ^ t = λ ) = p x ( λ ∣ s t − 1 ) 那麽,error 就是:
定義 q_t,是第 t 個 bit 的預測的錯誤率。
e t = [ [ s ^ t ≠ s t ] ] e_t=[[\hat s_t \ne s_t]] e t = [[ s ^ t = s t ]] q t = 1 − p x ( s t ∣ s t − 1 ) q_t=1-p_x(s_t|s_{t-1}) q t = 1 − p x ( s t ∣ s t − 1 ) 所以我們對整個字符串的預測錯誤率是:
E ∑ t = 1 T e t = ∑ t = 1 T q t = ∑ t = 1 T ( 1 − p x ( s ‾ t ) p x s ‾ t − 1 ) \mathbb{E}\sum_{t=1}^Te_t=\sum_{t=1}^Tq_t=\sum_{t=1}^T (1-\frac{p_x(\underline s_t)}{p_x{\underline s_t-1}}) E t = 1 ∑ T e t = t = 1 ∑ T q t = t = 1 ∑ T ( 1 − p x s t − 1 p x ( s t ) ) *這裏不是大家覺得理所當然的 連乘錯誤率 因爲我們定義 p_x 總是基於之前的結果。所以實際 predict 的時候每次都看了前面已經做出的全部結果。
???→
E ∑ t = 1 T e t = ∑ t = 1 T q t = ∑ t = 1 T ( 1 − p x ( s ‾ t ) p x s ‾ t − 1 ) ≤ ∑ t − 1 T − l n p x ( s ‾ t ) p x ( s ‾ t − 1 ) = − l n p x ( s ‾ T ) + l n p x ( s ‾ t ) … \mathbb{E}\sum_{t=1}^Te_t=\sum_{t=1}^Tq_t=\sum_{t=1}^T (1-\frac{p_x(\underline s_t)}{p_x{\underline s_t-1}})\le\sum_{t-1}^T-ln\frac{p_x(\underline s_t)}{p_x(\underline s_{t-1})}=-lnp_x(\underline s_T)+lnp_x(\underline s_t)\dots E t = 1 ∑ T e t = t = 1 ∑ T q t = t = 1 ∑ T ( 1 − p x s t − 1 p x ( s t ) ) ≤ t − 1 ∑ T − l n p x ( s t − 1 ) p x ( s t ) = − l n p x ( s T ) + l n p x ( s t ) … 這個不等式是考慮說產生 2^T+2^T-1+....=M 種的全部 program 中肯定有一個是對的,那我們的錯誤率肯定是小於 1/M,如果 T 趨近於無限,則 M 趨近於無限,那麽我們的 error rate 應該趨近於 1, learning impossible.
再定義
K x ( s ‾ T ) = m i n { ∣ P ∣ : s ‾ t × v ‾ } K_x (\underline s_T)=min\{|P|:\underline s_t \times \underline v\} K x ( s T ) = min { ∣ P ∣ : s t × v } 那:
e r r o r ≤ − l n 2 − K x ( s ‾ T ) = K x ( s ‾ t ) × l n 2 error\le -ln2^{-K_x(\underline s_T)}=K_x(\underline s_t)\times ln2 error ≤ − l n 2 − K x ( s T ) = K x ( s t ) × l n 2 上面的意思是最大極限的一堆 ln 裏有一個最短的 program P,已經生成了目標字串。
綜上,我們發現 error≤ \le ≤
且平均錯誤率:
e r r o r ˉ ≤ K x ( s ‾ t ) l n 2 T \bar {error}\le \frac {K_x(\underline s_t)ln2}{T} error ˉ ≤ T K x ( s t ) l n 2 上式表示 prediction 的 upper bound.
*consider hypothesis set :
H = { h } \mathcal{H}=\{h\} H = { h } and examples :
D = { ( x n , y n = h ∗ ( x n ) } ( i n p u t ( f e a t u r e ) , o u p u t ( l a b e l ) ) D=\{(x_n,y_n=h_*(x_n)\}(input(feature),ouput(label)) D = {( x n , y n = h ∗ ( x n )} ( in p u t ( f e a t u re ) , o u p u t ( l ab e l )) and
∃ h ∗ ∈ H \exist h_*\in \mathcal{H} ∃ h ∗ ∈ H define all x n x_n x n
對應關係是:
programs→hypotheses
generating programs → h_*
errors → e ( h ) = E x p ˜ ( x ‾ ) [ [ h ( x ‾ ) ≠ h ∗ ( x ‾ ) ] ] e(h)=\mathbb{E_{x\~p(\underline x)}}[[h(\underline x)\ne h_*(\underline x)]] e ( h ) = E x p ˜ ( x ) [[ h ( x ) = h ∗ ( x )]]
PAC:
get g w/ small :(我們在 hypothesis 裏拿一個 g ,這個 g 的 error 有上限而且準確度還可以)
e ( g ) ≤ “ ϵ ” e(g)\le“\epsilon” e ( g ) ≤ “ ϵ ” or
p r o b ≥ 1 − δ o v e r g e n e r a t i o n o f D prob \ge 1-\delta ~over~generation~of~D p ro b ≥ 1 − δ o v er g e n er a t i o n o f D see http://blog.pluskid.org/?p=821 ??
*if always pick g ∈ H g\in \mathcal{H} g ∈ H
g ( x ‾ n ) = y n f o r a l l n ( z e r o t r a i n i n g e r r o r ) g(\underline x_n)=y_n~for~all~n(zero~training~error) g ( x n ) = y n f or a ll n ( zero t r ainin g error ) //PROOF HERE AND ABOVE、
PROOF
key: e D ( h ) = σ e_D(h)=\sigma e D ( h ) = σ
if N is large enough, atypical < δ p ( h ) <\delta p(h) < δ p ( h )
e D ( h ) = 0 , e ( h ) ≤ 1 N ( l n 1 δ + l n 1 p ( h ) ) ≥ 1 − δ e_D(h)=0,e(h)\le\frac{1}{N}(ln\frac{1}{\delta}+ln\frac{1}{p(h)})\ge1-\delta e D ( h ) = 0 , e ( h ) ≤ N 1 ( l n δ 1 + l n p ( h ) 1 ) ≥ 1 − δ ,
CONCLUSION
if having a preference(aka prior) p(h) on h ∈ H h\in \mathcal{H} h ∈ H
p ( h ) ≥ 0 , ∑ h p ( h ) = 1 p(h)\ge0,\sum_h p(h)=1 p ( h ) ≥ 0 , h ∑ p ( h ) = 1 then for any given 0 ≤ δ ≤ 1 0\le\delta\le1 0 ≤ δ ≤ 1
D ∼ p N ( x ‾ ) p r ( e ( g ) ≤ 1 N ( l n 1 δ + l n 1 p ( g ) ) ) ≥ 1 − δ ^{p_r}_{D\sim p^N(\underline x)}(e(g)\le \frac{1}{N}(ln\frac{1}{\delta}+ln\frac{1}{p(g)}))\ge 1-\delta D ∼ p N ( x ) p r ( e ( g ) ≤ N 1 ( l n δ 1 + l n p ( g ) 1 )) ≥ 1 − δ 大概意思是是找比較簡單的 h,(Occam’s Razor)來丟進去,在 N 沒那麽大的時候可以控制學習的錯誤率。p(h)是preference
h 不複雜,preference 就大一點。這樣在 N 情況下控制錯誤率。
也許要用短小的 hypothesis 來 learn←→ 也許需要用小的 codeword 來 encode
H o w m a n y b i t s ? How~many~bits? Ho w man y bi t s ? Shannon Entropy
StoreH ( X ) ≈ 1 N H δ ( X N ) ≤ H 0 ( X ) H(X)\approx\frac{1}{N}H_\delta(X^N)\le H_0(X) H ( X ) ≈ N 1 H δ ( X N ) ≤ H 0 ( X ) Approximatem i n q : d ˉ ≤ D I ( X ; Y q ) min_{q:\bar d\le D}I(X;Y_q) mi n q : d ˉ ≤ D I ( X ; Y q ) Commute(Way to Modern Communication) m a x q I ( X q ; Y q ) max_qI(X_q;Y_q) ma x q I ( X q ; Y q )